本节书摘来异步社区《LDA漫游指南》一书中的第2章，第2.4节，作者： 马晨，更多章节内容可以访问云栖社区“异步社区”公众号查看

2.4　多项分布(multinomial distribution)

多项分布[1]是二项分布的推广扩展，在n次独立试验中每次只输出k种结果中的一个，且每种结果都有一个确定的概率p。多项分布给出了在多种输出状态的情况下，关于成功次数的各种组合的概率。

举个例子，投掷n次骰子，这个骰子共有6种结果输出，且1点出现概率为p_1，2点出现概率p_2，……多项分布给出了在n次试验中，骰子1点出现x_1次，2点出现x_2次，3点出现x_3次，…，6点出现x_6次。这个结果组合的概率为

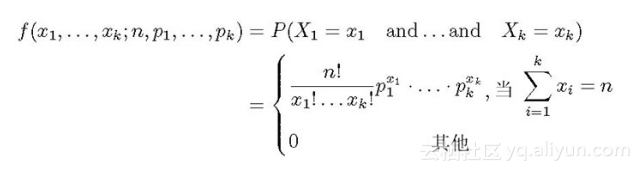
式(2.8)为多项分布的概率公式，注意在这个公式中，x_i为第i种状态的输出结果的频度，如果k=2，只有两种情况，此公式将退化为二项分布，所以二项分布是特殊情况下的多项分布。

也可以用gamma函数表示（这个写法的形式和Dirichlet分布相似）：

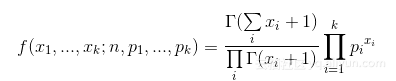
下面通过一个例题加深对多项分布的印象:

问题

同时投掷5枚骰子，出现两对点数一样的概率是多少？解：现在先把问题简化成特定投掷到2个一点，2个二点，1个三点的概率是多大？

X_1～X_6表示6个点的出现次数之和为5，则

先不考虑2，2，1三者顺序时共有left( {begin{array}{*{20}{c}}6\3end{array}} right)种取法；再考虑下2，2，1三者交换顺序有3种，因为两个2先后交换仍为2，2。

所以X_1～X_6，其中2个取2，1个取1的种类有3 cdot left( {begin{array}{*{20}{c}}6\3end{array}} right) = 60种。

最后的答案是，概率为60 cdot frac{5}{

{1296}} = frac{ {25}}{ {108}}。

多项分布的极大似然估计

需要特别说明的是，“多项分布的似然函数”容易让读者困惑。这里特别说明一下，我们将多项分布的概率公式(2.8)重新写下来：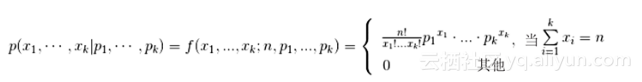

注意这个公式中的x_i种状态的输出结果的频度，其出现在指数部分，每个状态的可能性为p_1，p_2，…，p_k，且sumnolimits_{i = 1}^k {

{p_i}} = 1 。在极大似然估计中，由于使用log形式的似然函数（log-likelihood），随后对其求导，获取似然函数的极值。在这个过程中，多项式系数作为常数项通常被无情地忽略了，我们做如下分析：

根据极大似然估计的原理，对于确定的n次试验结果，多项分布的似然函数满足：

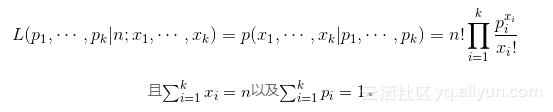
接着使用log-likelihood技法:

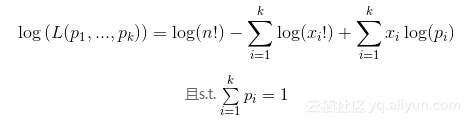
引入拉格朗日乘数法（如果不了解拉格朗日乘数法，可参阅6.1.4节），则

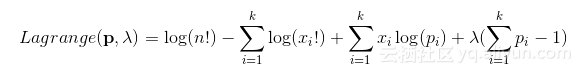
紧接着对其按照参数p求导，前两项不含p，求导得0，被忽略，由此公式(2.8)多项式系数作为常数项就都被忽略了。

直观思考一下多项分布的极大似然估计，其实可想而知，就是数数x_i的个数，然后算一下占整个样本中的比例就可以作为p_i概率的估计了。所以通常在使用似然函数时，可以忽略其常数项—多项式系数。